Note: This page describes the KCH half adder project. The project consists of a special PCB that realizes one half adder using NAND gates, where some of the on-board components are left to be soldered by students as an exercise. Multiple PCBs can be connected to each other to form full adders or multi-bit carry ripple adders. In addition to the PCB, we provide detailed documentation explaining the theory involved for both the PCB design and the digital circuit realization. As the intended target audience is school students and their teachers, the rest of this page and documentation is currently only available in German.

Diese Seite stellt die KCH Halbaddierer Platine und die dazugehörige Theorie vor. Die Platine ist als Lehrprojekt für Schüler gedacht und zeigt, wie im Chipdesign digitale Addierer für Binärzahlen realisiert werden. Zusätzlich zeigen wir, in welchen Lehrveranstaltungen Kenntnisse zu den verschiedenen Themen vertieft werden können.

Um neben der Theorie auch praktische Erfahrungen zu vermitteln, ist die Platine als Lötübung ausgeführt: Nicht alle Bauteile sind komplett bestückt und die fehlenden Teile müssen von den Schülern selbst auf die Platine gelötet werden. Als Open-Hardware Projekt sind alle Daten zur Platine frei verfügbar und Interessierte können sich jederzeit eigene Platinen fertigen und bestücken lassen. Die Beschreibung auf dieser Seite richtet sich größtenteils an Schüler und Anwender allgemein. Weitere Informationen und Unterlagen für Lehrkräfte werden am Ende dieser Seite verlinkt.

Zusammenbau der Platine

Stückliste

Zum Zusammenbau der Platine werden die folgenden Bauteile benötigt:

1. 1x Unbestückte KCH Halbaddierer Platine

   

2. 2x 74HC00 ICs mit DIP-14 Gehäuse
   

3. 2x ESP1010 Miniatur Schiebeschalter
   

Bestücken der ICs

Es empfiehlt sich, zuerst niedrigere Bauteile und danach höhere Bauteile zu bestücken: Bauteile können dann einfach auf die Platine gesteckt und diese umgedreht und mit der Vorderseite auf den Tisch gelegt werden. Die losen Bauteile liegen dann auf den Tisch auf und fallen nicht aus der Platine heraus.

Bevor die ICs bestückt werden müssen, müssen die Beinchen von diesen ICs noch etwas in Form gebogen werden: Normalerweise sind die Pins von DIP ICs etwas aufgebogen und müssen schmaler gebogen werden. Am einfachsten geht dies mit einer speziellen Biegezange.

Beim Einstecken der ICs in die Platine muss die Ausrichtung beachtet werden: Die Pins der ICs haben im Allgemeinen verschiedene Funktionen und dürfen nicht vertauscht werden. Im Datenblatt der ICs ist aus diesem Grund eine Nummerierung der Pins gegeben. Zur einfacheren Ausrichtung der ICs werden diese auf den Bestückungsdruck der Platine und auf den ICs markiert: Auf unserer Platine ist die kurze Seite, an der Pin 1 liegt mit einem Ring markiert. DIP ICs wie unsere 74HC00 haben eine Aussparung auf der Oberseite, die diese Form hat. Das IC muss also so gedreht werden, dass diese Aussparung mit dem Bestückungsdruck übereinstimmt. Andere ICs haben andere Markierungen für die Ausrichtung, die Details dazu sind jedoch immer im dazugehörigen Datenblatt gegeben.

Wenn die ICs passend eingesteckt sind, kann die Platine umgedreht auf den Tisch gelegt werden. Die Beinchen der ICs können dann nacheinander verlötet werden. Dazu wird die Spitze des Lötkolbens so angesetzt, dass sie ein Beinchen und das dazugehörige Pad, die runde Metalloberfläche um das Beinchen auf dem PCB, berührt. Parallel dazu wird mit der anderen Hand das Lot an die Lötspitze und das Beinchen geführt.

Wenn das Pad auf der Platine mit größeren Metallflächen verbunden ist, kann es etwas dauern, bis das Pad und das Beinchen heiß genug werden und der Lötzinn schmilzt. Eine Gute Lötstelle sollte eine glatte, glänzende Oberfläche haben.

Bestücken der Schalter

Die Schalter werden nach dem selben Prinzip bestückt. Bei den hier verwendeten Schaltern muss die Ausrichtung nicht beachtet werden. Nachdem die Schalter bestückt wurden, sind die Beinchen auf der Unterseite noch etwas lang: Die Platine liegt dann nicht eben auf den Steckverbindern am Rand auf dem Tisch auf. Es empfiehlt sich also, diese Beinchen noch mit einem Seitenschneider zu kürzen. Achtung: Die abgezwickten Beinchen fliegen weit und können ins Auge gehen. Wenn der Teil der Beinchen, der abgezwickt werden soll, auf den Tisch zeigt, landet er nur dort.

Überprüfen der Ergebnisse

Bevor die Platine in Betrieb genommen wird, sollte geprüft werden ob alle Lötstellen richtig ausgeführt sind. Wichtig ist, dass alle Beinchen verlötet sind, nebeneinander liegende Beinchen und Pads nicht verbunden wurden und dass es keine kalten Lötstellen gib. Kalte Lötstellen sind Stellen, an denen nur die Beinchen, aber nicht die Pads verlötet wurden. Diese sehen wie eine richtige Lötstelle aus, verbinden die Teile aber nicht elektrisch. Kalte Lötstellen lassen sich oft an einer blassen Oberfläche oder Spitzen Ecken im Lötzinn erkennen.

Benutzen der Platinen

Eine einzelne Platine arbeitet als Halbaddierer. Sie kann für eine Stelle zwei Binärzahlen addieren, genannt a und b. Als Ergebnis bekommen wir aus dieser Schaltung eine Summe, s und einen Übertrag in die nächste Stelle, cout. Diese Werte werden auf der Platine über die im Bild unten markierten LEDs dargestellt. Jedem wert sind dabei zwei LEDs in unterschiedlichen Farben zugeordnet: Ist der Wert 0, leuchtet die blaue LED. Ist der Wert 1, leuchtet statt dessen die rote LED.

Damit die Schaltung funktionieren kann, muss diese mit Strom versorgt werden. Dazu kann einfach an den USB-C Stecker ein USB-Netzteil oder ein PC angeschlossen werden.

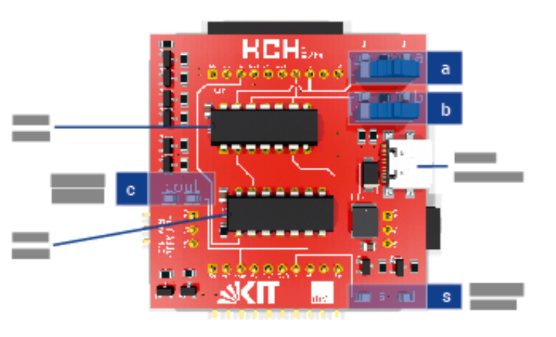
Um die Funktion der zusammengebauten Schaltung zu prüfen, können Eingangssignale über die Schalter eingestellt werden. Wenn wir z.B. Beide Schalter nach links auf 0 schieben, sollten die Eingänge a und b 0 sein und die Ausgänge s und cout ebenfalls. Es sollten also alle LEDs blau leuchten. Schieben wir a nach rechts, sollte für a die rote LED leuchten und zeigen, dass a nun 1 ist. Da 1 + 0 = 1, ist s = 1 und die LED für s sollte rot leuchten. Die LED für cout bleibt blau. Schieben wir jetzt auch den Schalter b nach rechts, ist 1 + 1 = 0 mit Übertrag 1. Es sollten also alle LEDs rot leuchten, bis auf die LED für s.

Zwei Platinen als Volladdierer

Wenn zwei PCBs übereinander zusammengesetzt werden, realisieren diese einen Volladdierer. Im Vergleich zum Halbaddierer hat der Volladdierer noch einen weiteren Eingang, cin. Dieser Eingang ist der Übertrag von der vorherigen Stelle. Ein Volladdierer kann also für die Addition einer jeden Stelle bei der Addition von mehrstelligen Zahlen verwendet werden. Die Stromversorgung erfolgt wie im vorherigen Fall über die USB-C Buchse. Dabei reicht es, eine USB-C Buchse anzuschließen. Die anderen Platinen werden mit von dieser mit Strom versorgt. Welche USB-C Buchse verwendet wird, ist egal.

Die Eingänge a und b werden auf der oberen Platine eingestellt. Die Schalter auf der unteren Platine haben in diesem Aufbau keine Funktion und ihre Position ist egal. Die Ergebnisse s und cout müssen jetzt auf der unteren Platine abgelesen werden. Auf der oberen Platine zeigen die LEDs jetzt Werte von internen Signalen, aber nicht die Endergebnisse. Der Übertrag cin kann nicht über Schalter eingestellt werden: Er wird automatisch von den Platinen rechts übernommen. Ist dort keine Platine eingesteckt, ist cin fest auf 0 gelegt. Im einfachen Fall mit 2 Platinen können wird die Funktion des Volladdierers also nicht wirklich zeigen. Es können aber die Beispiele für den Halbaddierer oben auch mit dem Volladdierer nachgestellt werden, um zu sehen dass die Ergebnisse wirklich an den LEDs auf der unteren Platine anlegen.

Mehrere Platinen als Carry Ripple Addierer

Um die Funktion mit Überträgen zu sehen, brauchen wir mindestens 4 Platinen. Hier zeigen wir statt dessen einen Aufbau mit 6 Platinen: Dieser 3-bit Carry-Ripple Addierer kann zwei Binärzahlen mit je 3 Bit addieren. Die Stromversorgung erfolgt wieder über einen der USB-Ports rechts. Die Eingänge a und b werden wieder auf den oberen Platinen eingestellt, die Schalter auf den unteren Platinen sind ohne Funktion. Die Ergebnisse s und cout werden ebenfalls wieder auf der unteren Platine abgelesen.

Im Gegensatz zu dein ersten Beispielen, gibt es nun jeden Eingang und jeden Ausgang dreifach: Die erste Stelle (0) von a und b wird auf der Platine ganz rechts oben eingestellt. Die Ergebnisse s und cout für diese erste Stelle sind dann auf der Platine rechts unten. Die zweite Stelle (1) findet man dann auf den mittleren Platinen und die dritte Stelle (2) ganz links.

Als Beispiel wollen wir nun die Binärzahlen 011 und 011 addieren: Von links nach rechts stellen wir für die Schalter von a und b also jeweils 0, 1 und 1 ein. Wie erwartet sehen wir für Stelle 0 (rechts) 1 + 1 = 0 Übertrag 1. Für Stelle 1 (Mitte) haben wir 1 + 1 + 1 (eingehender Übertrag) = 1 Übertrag 1. Für die Stelle 2 (links) folgt dann 0 + 0 + 1 = 1 Übertrag 0.

Hintergrund: Binäre Addition

Wie funktioniert nun die Schaltung auf der Platine? Hierfür müssen wir uns die Theorie zur binären Addition ansehen.

Die Addition von Binärzahlen kann wie beim Schriftlichen Addieren von Dezimalzahlen stellenweise durchgeführt werden. Ein Beispiel für die Addition der zwei Dezimalzahlen 39 und 3 ist hier gezeigt:

Hierbei wird zuerst die Stelle 0 addiert. Die Summe für diese Stelle ist  9 + 3 = 2, der Übertrag in die nächste Stelle ist 1. In Stelle 1 wird folglich 3 + 0 + 1 = 4 addiert und es gibt keinen weiteren Übertrag.

Die Abbildung oben zeigt das Prinzip der stellenweisen Addition für binär dargestellte Zahlen, wie sie in der Digitaltechnik üblich sind. Für Stelle 0 ergibt sich 1 + 1 = 0 mit Übertrag 1. In Stelle 1 folgt demnach 1 + 1 + 1 = 1 mit Übertrag 1. In der letzten Stelle ergibt sich abschließend 0 + 0 + 1 = 1. An diesem Beispiel sieht man, dass bei der stellenweisen Addition für jede Stelle drei Ziffern (einstellige Zahlen) addiert werden. Eine dieser Zahlen ist hierbei der Übertrag aus der vorherigen Stelle und wird für Stelle 0 dementsprechend nicht benötigt.

Funktionstabellen

Um die Logik zur Addition einer Stelle zu beschreiben, können wir die  in der Digitaltechnik üblichen Funktionstabellen verwenden. Die folgende Abbildung zeigt die Tabelle für die Addition der Stelle 0:

Hierbei stehen die Operanden als Eingangsvariablen a und b in den zwei linken Spalten. Die Ausgangsvariablen Übertrag c und Summe s folgen in den nächsten zwei Spalten. In der Tabelle sind alle Eingangskombinationen für die Operanden a und b gegeben. Liegen an den Eingängen die in der Zeile angegebenen Werte an, müssen die Ausgänge die in der Zeile notierten Werte annehmen.​

Unser Beispiel von oben finden wir in der letzten Zeile wieder: 1 + 1 = 0 mit Übertrag 1.​ Eine Schaltung in binärer Logik mit zwei Eingangsvariablen wird durch eine Tabelle mit vier Zeilen vollständig beschrieben.​

Notation  und Grundoperationen​

Zur weiteren Analyse stellen wir die Funktion in Boolescher Algebra dar. Dafür verwenden wir die hier gezeigten Operatoren:

Anhand der Funktionstabellen sehen wir, dass der Übertrag c einer AND Operation entspricht, die Summe s einem XOR. Die AND Operation gibt nur dann eine 1 zurück, wenn beide Eingänge 1 sind. Die XOR Operation ist ein exklusives OR und gibt dann 1 zurück, wenn genau ein Eingang 1 ist. Zusätzlich zu diesen Operation sind die grundsätzlichen Operationen OR, NOT und NAND gezeigt. Für alle Operationen sind auch die algebraische und symbolische Darstellung gezeigt.

Realisierung durch NAND Gatter​

Überführen wir die Tabelle in die symbolische Notation, erhalten wir diese Schaltung:

Überführen wir die Summe s in die algebraische Notation, können wir auch hier die XOR Operation verwenden. Alternativ kann diese Operation aber auch durch NOT, AND und OR Operationen dargestellt werden. Wir erhalten dann die erste Zeile hier:​

In der Digitaltechnik wird oft der Umstand genutzt, dass alle Booleschen Funktionen nur durch NANDs darstellbar sind. So wird beispielsweise auch das KCH Halbaddierer PCB rein mit NANDs realisiert. Mit speziellen Umformungen (doppelte Negation und De Morgansche Regel) können wir die Summenfunktion durch NAND Operationen darstellen. Um NOT Operationen mit NANDs umzusetzen, werden beide Eingänge des NANDs mit dem selben Signal verbunden. Zur Berechnung der Summe s mit NANDs ergibt sich dann diese Schaltung:

Halb- und Volladdierer

Die zu vorherige Schaltung besteht aus 5 NAND Gattern. Durch weitere Umformungen in  sehen wir, dass auch 4 Gatter genügen:

Wenn nun auch der Übertrag c realisiert wird, erhalten wir die auf dem KCH Halbaddierer PCB benutzte Schaltung:

Bisher haben wir nur Stelle 0 betrachtet. Hierfür genügt ein Halbaddierer, da kein eingehender Übertrag (cin) nötig ist. Für die weiteren Stellen ist ein Volladdierer nötig, der wie folgt realisiert wird:

Carry-Ripple​ Addierer

Um beliebig viele Stellen zu addieren, kombiniert man Halb- und Volladdierer wie folgt:

Die Stellen der ersten Zahl wurden a0, a1, a2 genannt, die der zweiten b0, b1, b2 und die des Ergebnisses s0, s1 und s2. Überträge wurden entsprechend den Eingängen als c1 und c2 bezeichnet. Die gesamte Schaltung wird als Carry-Ripple Addierer bezeichnet und kann wie hier erklärt rein aus NANDs realisiert werden.

Erklärungen zum Schaltplan

Im folgenden wir der Schaltplan zur Platine erklärt. Hierbei werden nicht nur die von den Schülern bestückten Bauteile berücksichtigt, sondern auch der vorbestückte Teil  im Detail erklärt.

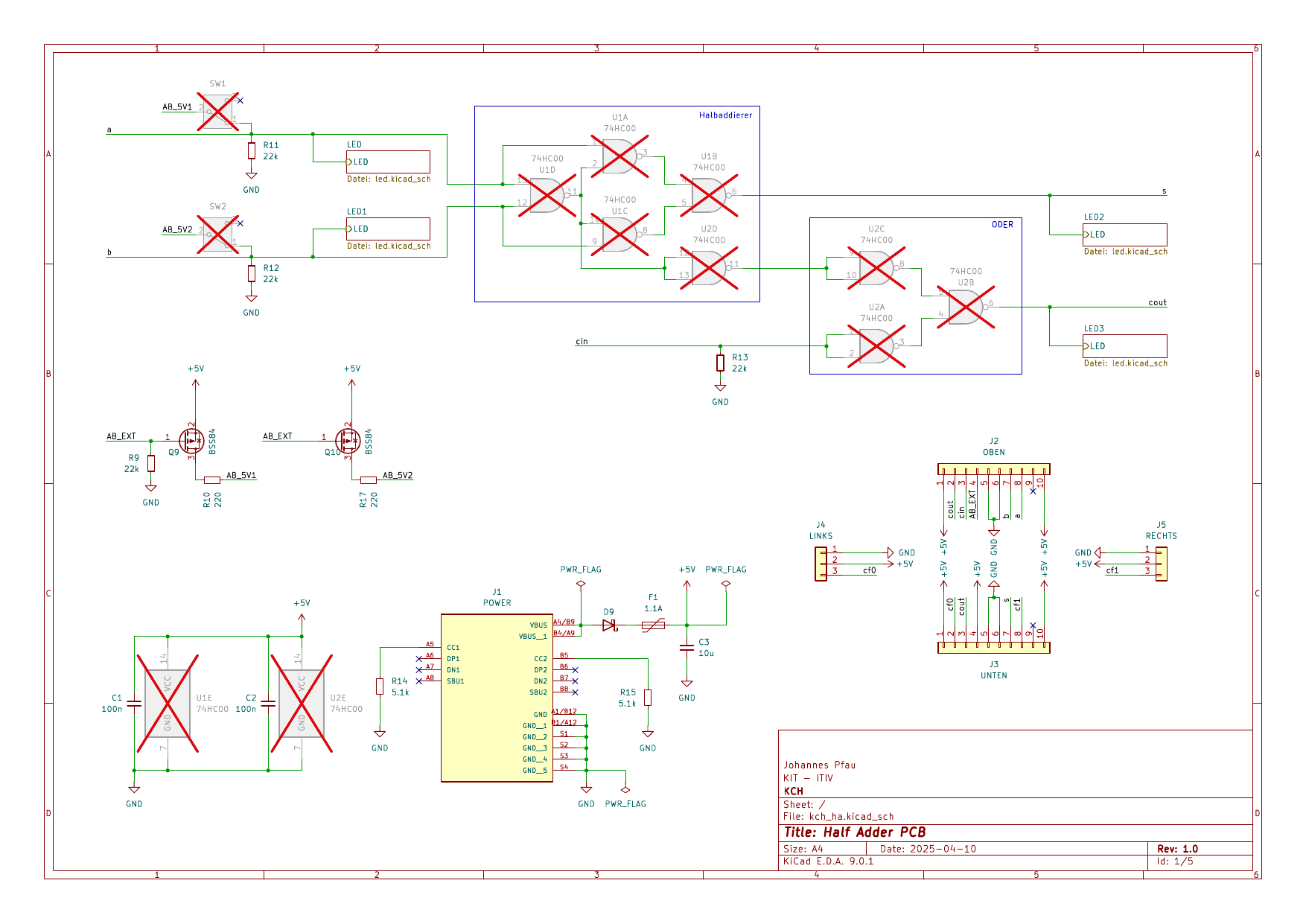
Halb - und Volladdierer

Die Halbaddierer Funktion wird durch die NANDs U1A-U1D und U2D der 74HC00 Gatter U1 und U2 realisiert. Das Carry des Halbaddierers wird in den Gattern U2A-U2C mit dem cout Signal der Platine darüber ODER-verknüpft, um den Volladdierer zu realisieren.

Ist am oberen Stecker keine Platine eingesteckt, zieht R13 als Pulldown-Widerstand das cin Signal auf 0. Es gilt:

damit wird in diesem Fall das Carry Out des Halbaddierers auf der Platine unverändert an cout gegeben. Die Platine funktioniert als Halbaddierer.

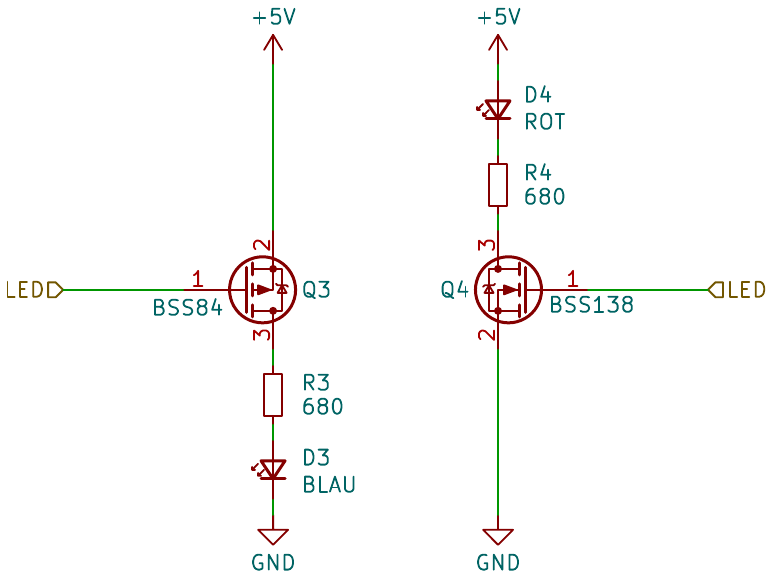
LEDs für Signale

Alle Signale werden mit LEDs dargestellt. Das Signal liegt auf den Gates der MOSFETs Q3 und Q4. Bei High-Pegel sperrt der p-Kanal MOSFET Q3, D3 leuchtet nicht. Der n-Kanal MOSFET Q4 leitet, D4 leuchtet. Bei Low-Pegel leitet Q3 und Q4 sperrt. D3 leuchtet, D4 nicht.

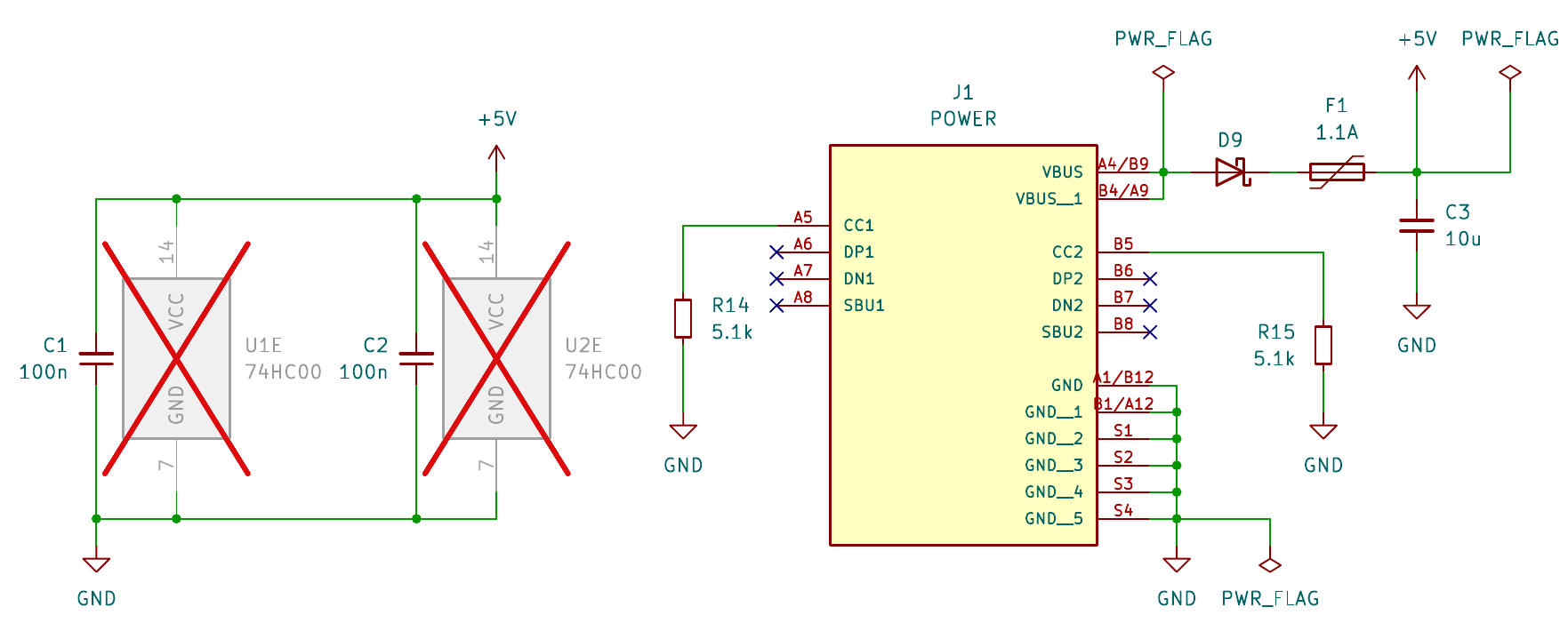
Stromversorgung

C1 und C2 sind Entkopplungskondensatoren für die 74HC00 Logik-ICs. Die USB-C Buchse J1 ist mit den Widerständen R15 und R14 nach USB Standard verbunden. Die Schottky-Diode D9 erlaubt den Stromfluss nur in eine Richtung, sodass über die USB-Buchse gespeist werden kann, aber ein Stromfluss in das Netzteil verhindert wird. So werden Netzteile geschützt, wenn mehrere Platinen verbunden werden. F1 ist eine Selbstrückstellende Sicherung: Tritt ein Kurzschluss in der Schaltung auf, unterbricht diese den Stromfluss. Ist der Kurzschluss behoben, leitet die Sicherung wieder. C3 verhindert als Stützkondensator einen Spannungsabfall bei kurzzeitigen Stromspitzen.

Eingangssignale und PCB-Steckverbinder

Die Steckverbinder J2 bis J5 verbinden mehrere Platinen. Neben den Spannungsversorgungen übertragen diese auch mögliche Eingangssignale: Ist an J2 keine Platine verbunden, werden die  Eingangssignale a und b über die Schalter SW1 und SW2 sowie die Pulldown-Widerstände R11 und R12 eingestellt. Die Widerstände ziehen das Signal hochohmig auf Low-Pegel, die Schalter können diese hochohmigen Pegel aber auf High-Pegel überschreiben. AB_EXT liegt durch R9 auf Low-Pegel, die p-Kanal MOSFETs Q9 und Q10 leiten und an AB_5V1 und AB_5V2 liegen 5V an.

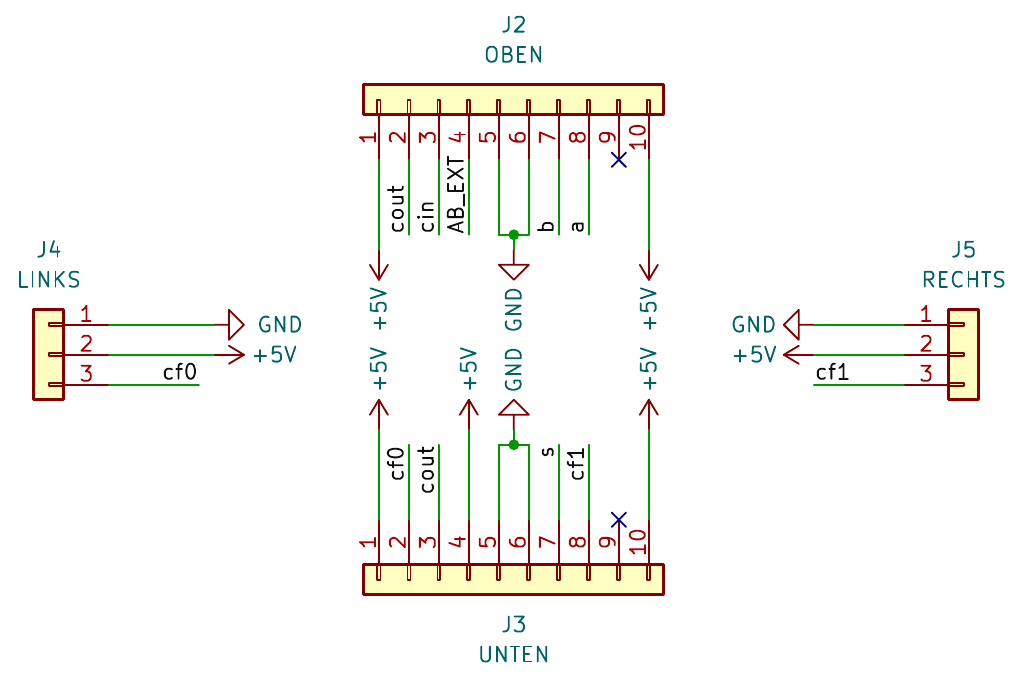
Ist an J2 (oben) eine andere Platine verbunden, wird das Signal AB_EXT über Pin 5 von J3 dieser Platine auf 5V gezogen.  Diese Spannung liegt an den Gates von Q9 und Q10 an, wodurch die Transistoren sperren. Die Signale AB_5V1 und AB_5V2 an den Schaltern SW1 und SW2 sind hochohmig und die Schalter können die Eingänge a und b nicht mehr auf High-Pegel ziehen. Sie werden somit auf der unteren Platine deaktiviert und haben keine Wirkung. Die Eingänge a und b werden stattdessen von den Ausgängen der oberen Platine übernommen und überschreiben die Low-Pegel der Widerstände R11 und R12, um den Volladdierer zu realisieren.

Kombination von Platinen

Wie bereits erklärt können zwei Platinen zu einem Volladdierer verbunden werden. Weiterhin können Addierer für Binärzahlen mit mehreren Bits als Carry-Ripple Addierer realisiert werden. In dieser Konfiguration berechnet ein Volladdierer jeweils eine Stelle der Summe. An jeder Stelle entsteht weiterhin ein Übertrag (Carry), der an die nächste Stelle übergeben werden muss. Werden Platinen auch seitlich zusammengesteckt, werden die Signale wie folgt verbunden:

Hier sieht man, wie die Ausgänge der oberen Platinen mit den Eingängen der unteren verbunden werden, um den Volladdierer zu realisieren. Auch sieht man, wie AB_EXT angesteuert wird. Das Carry Out Signal jedes Volladdierers wird auf der unteren Platine auf den cout Pin geführt, und muss für die nächste Stelle der Summe an die Platine links, an Eingang a weitergegeben werden.

Weiterführende Informationen

Die Grundlagen und die Verwendung der Boolschen Algebra und die Darstellung in NANDs wird im KIT Elektrotechnikstudium in der Veranstaltung Digitaltechnik behandelt. Weitere Informationen zur Funktion und zu Alternativen zu der vorgestellten Addiererschaltung und zu weiteren Digitalschaltungen im Chipdesign werden in der Vorlesung Mikroelektronische Schaltungen und Systeme vorgestellt. PCB-Design, sowohl das Erstellen von Schaltplänen als auch das Erstellen von PCB-Layouts, wird im Labor Schaltungsdesign gelehrt. Dabei werden als Teil des Labors PCBs entworfen, gefertigt und selbst bestückt.

Weitere Informationen zu den zu bestückenden Bauteilen findet man in den Datenblättern: Hier für das 74HC00 NAND IC und hier für den ESP1010 Schiebeschalter.

Den Schaltplan und das Layout als KiCAD Projekt findet ihr als Open Hardware Projekt auf unserer Github Präsenz: github.com/kit-kch/ha-pcb.